使用向量移动物体
向量是基本数学概念,允许你描述方向和大小。在游戏和应用中,向量通常用于描述基本属性,例如角色的位置、物体移动的速度或两个物体之间的距离。
向量算术是计算机编程许多方面的基础,例如图形、物理和动画,深入了解它有助于充分利用 Unity。
向量可以表示在多个维度,Unity 提供了 Vector2、Vector3 和 Vector4 类用于处理 2D、3D 和 4D 向量。这三种类型的 Vector 类都共享许多相同的函数,例如大小,因此本页上的大多数信息都适用于所有三种类型的 Vector,除非另有说明。
本页概述了 Vector 类及其在脚本中的常见用途。有关向量类每个成员的详尽参考,请参阅 Vector2、Vector3 和 Vector4 的脚本参考页面。
了解向量算术
加法
当两个向量相加时,结果等效于将原始向量作为“步长”,一个接一个。请注意,两个参数的顺序无关紧要,因为结果无论如何都是相同的。
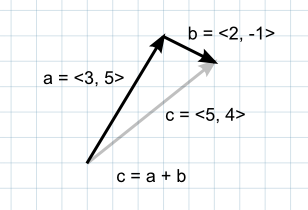
如果第一个向量被视为空间中的一个点,那么第二个向量可以被解释为从该位置的偏移量或“跳跃”。例如,要找到地面位置上方 5 个单位的点,可以使用以下计算
var pointInAir = pointOnGround + new Vector2(0, 5);
如果向量表示力,那么从它们的“方向”和“大小”(大小表示力的尺寸)来思考它们会更直观。添加两个力向量会产生一个新的向量,等效于力的组合。这个概念在同时应用具有多个独立分量的力时通常很有用(例如,向前推进的火箭也可能受到横风的影響)。
此处的示例使用 2D 向量,但相同的概念也适用于 3D 和 4D 向量。
减法
向量减法最常用于获取从一个物体到另一个物体的方向和距离。请注意,减法时两个参数的顺序确实很重要。
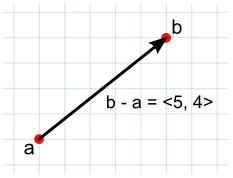
// The vector d has the same magnitude as c but points in the opposite direction.
var c = b - a;
var d = a - b;
与数字一样,添加向量的负数与减去正数相同。
// These both give the same result.
var c = a - b;
var c = a + -b;
向量的负数与原向量的大小相同,并且沿同一条线但方向完全相反。
从一个物体到另一个物体的方向和距离
如果空间中的一个点从另一个点中减去,那么结果将是一个指向从一个物体到另一个物体的向量。
// Gets a vector that points from the player's position to the target's.
var heading = target.position - player.position;
除了指向目标物体方向之外,此向量的“大小”还等于两个位置之间的距离。你可能需要一个“归一化”向量,它给出指向目标的方向,但具有固定的距离(例如,用于引导弹丸)。你可以通过将向量除以它自己的大小来归一化向量。
var distance = heading.magnitude;
var direction = heading / distance; // This is now the normalized direction.
这种方法优于分别使用大小和归一化属性,因为它们都是 CPU 密集型(它们都涉及计算平方根)。
如果你只需要使用距离进行比较(例如,进行接近度检查),那么你可以完全避免大小计算。sqrMagnitude 属性给出大小值的平方,并且像大小一样计算,但没有耗时的平方根运算。与其将大小与已知距离进行比较,不如将平方大小与平方距离进行比较。
if (heading.sqrMagnitude < maxRange * maxRange) {
// Target is within range.
}
这比在比较中使用真实大小要高效得多。
有时,在 3D 中工作时,你可能需要一个到目标的“地面航向”。例如,想象一个站在地面上的玩家,需要靠近空中漂浮的目标。如果你从目标位置减去玩家位置,那么结果向量将向上指向目标。这对于调整玩家的变换来说并不合适,因为它们也会向上指;真正需要的是从玩家位置到目标正下方地面位置的向量。你可以通过获取减法的结果并将 Y 坐标设置为零来获得此向量。
var heading = target.position - player.position;
heading.y = 0; // This is the overground heading.
标量乘法和除法
在讨论向量时,通常将普通数字(例如,浮点值)称为标量。这意味着标量只有“尺度”或大小,而向量既有大小又有方向。
将向量乘以标量会导致一个指向与原始向量相同方向的向量。但是,新向量的“大小”等于原始大小乘以标量值。
同样,标量除法将原始向量的“大小”除以标量。
当向量表示运动偏移量或力时,这些操作很有用。它们允许你在不影响向量方向的情况下改变向量的“大小”。
当任何向量除以它自己的“大小”时,结果是一个“大小”为 1 的向量,称为归一化向量。如果将归一化向量乘以标量,则结果的“大小”将等于该标量值。当力的方向恒定但强度可控时,这很有用(例如,汽车车轮的力始终向前推,但动力由驾驶员控制)。
点积
点积取两个向量并返回一个标量。这个标量等于两个向量的“大小”相乘,然后结果再乘以向量之间的角度的余弦。当两个向量都归一化时,余弦基本上表示第一个向量在第二个向量方向上扩展的程度(反之亦然——参数的顺序无关紧要)。
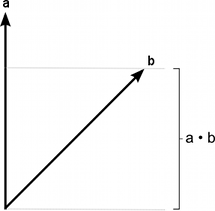
在下面,你可以看到与参考向量相比,不同角度的向量如何返回 1 到 –1 之间的点积值。
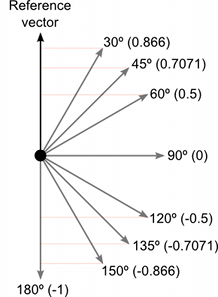
点积是一个比计算余弦更简单的数学运算,因此它可以在某些情况下代替 Mathf.Cos 函数或向量大小运算(它不能做完全相同的事情,但有时效果是等效的)。但是,计算点积函数所花费的 CPU 时间要少得多,因此它可以成为宝贵的优化手段。
如果你想计算一个向量“大小”在另一个向量方向上的分量,点积非常有用。
例如,汽车的速度计通常通过测量车轮的转速来工作。汽车可能不是直接向前移动(例如,它可能在侧向滑行),在这种情况下,部分运动将不在汽车朝向的方向上——因此不会被速度计测量。物体的 rigidbody.velocity 向量的大小将给出它总体运动方向上的速度,但要隔离向前方向上的速度,你应该使用点积
var fwdSpeed = Vector3.Dot(rigidbody.velocity, transform.forward);
方向可以是任何你喜欢的方向,但此计算中方向向量必须始终是归一化的。结果不仅比速度的大小更准确,而且还避免了查找大小时涉及的缓慢平方根运算。
叉积
叉积只有对 3D 向量才有意义。它将两个 3D 向量作为输入,并返回另一个 3D 向量作为结果。
结果向量垂直于两个输入向量。你可以使用“右手螺旋定则”来记住输出向量的方向,以及输入向量的顺序。如果你能按输入向量的顺序弯曲你的手指,你的拇指指向输出向量的方向。如果参数的顺序颠倒,那么结果向量将指向完全相反的方向,但将具有相同的大小。
结果的大小等于输入向量的“大小”相乘,然后该值再乘以它们之间的角度的正弦。下面显示了一些正弦函数的有用值:-
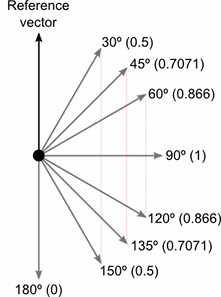
叉积可能看起来很复杂,因为它在返回值中结合了几个有用的信息。但是,与点积一样,它在数学上非常高效,可以用于优化原本依赖于更慢的超越函数(如正弦和余弦)的代码。
计算法线/垂直向量
在 网格Unity 的主要图形基本体。网格构成 3D 世界的很大一部分。Unity 支持三角形或四边形多边形网格。Nurbs、Nurms、细分曲面必须转换为多边形。更多信息
参见 术语表 生成过程中经常需要“法线”向量(即垂直于平面的向量),它在路径跟踪和其他情况下也很有用。给定平面上三个点,例如网格三角形的角点,你可以按以下方式找到法线:- 选择三个点中的一个 - 从另外两个点中分别减去它(产生两个新向量,“边 1”和“边 2”) - 计算向量“边 1”和“边 2”的叉积 - 叉积的结果是一个新的向量,它垂直于三个原始点所在的平面 - “法线”。
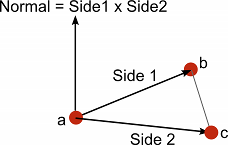
Vector3 a;
Vector3 b;
Vector3 c;
Vector3 side1 = b - a;
Vector3 side2 = c - a;
Vector3 normal = Vector3.Cross(side1, side2);
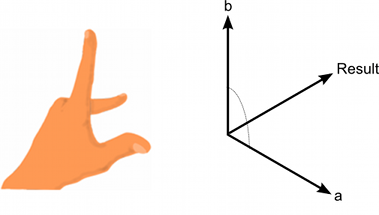
可以使用“左手定则”来决定将两个向量传递给叉积函数的顺序。当你向下看表面的顶端(法线将从那里向外指向)时,第一个向量应该按顺时针方向扫到第二个向量。
如果输入向量的顺序颠倒,结果将指向完全相反的方向。
对于网格,法线向量也必须是归一化的。这可以使用归一化属性来完成,但还有一些其他技巧偶尔有用。你还可以通过将其除以大小来归一化垂直向量:-
float perpLength = perp.magnitude;
perp /= perpLength;
另一个有用的说明是三角形的面积等于 perpLength / 2。如果你需要找到整个网格的表面积,或者想要根据它们的相对面积随机选择三角形,这将非常有用。