向量

向量是基本的数学概念，可以用来描述方向和大小。在游戏和应用程序中，向量通常用于描述一些基本属性，例如角色的位置、某个物体移动的速度或两个物体之间的距离。

向量算术是计算机编程许多方面的基础，例如图形、物理和动画，深入了解向量算术对充分利用Unity非常有用。

向量可以在多个维度中表达，Unity提供了Vector2、Vector3和Vector4类以处理2D、3D和4D向量。这三种类型的向量类共享许多相同的函数，例如模量，所以除非另有说明，本页面上大部分信息适用于所有三种类型的向量。

本页提供了向量类及其在脚本中常用概述。有关向量类每个成员的详尽参考，请参阅Vector2、Vector3和Vector4的脚本参考页面。

理解向量算术

加法

当两个向量相加时，结果是将原始向量作为“步子”，一个接一个地。请注意，两个参数的顺序并不重要，因为结果无论哪种方式都是相同的。

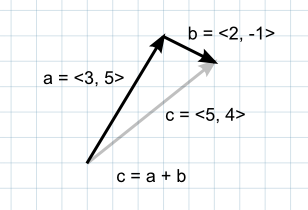
如果第一个向量被看作空间中的一个点，那么第二个可以解释为从这个位置开始的偏移或“跳跃”。例如，要找到一个比地面位置高5个单位的点，可以使用以下计算方式：

 var pointInAir = pointOnGround + new Vector2(0, 5);

如果向量代表力，那么更直观地，可以按其方向和大小（大小表示力的大小）来考虑它们。将两个力向量相加得到一个新的等于力的组合的向量。当同时应用由多个单独的分量组成的作用力时，这个概念非常有用（例如，被推动向前移动的火箭同时也可能受到横风的干扰）。

尽管这里显示的是2D向量示例，但相同的原理也适用于3D和4D向量。

减法

向量减法最常用于得到一个物体到另一个物体的方向和距离。请注意，减法时两个参数的顺序是重要的：

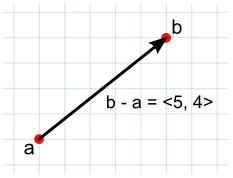
// The vector d has the same magnitude as c but points in the opposite direction.
var c = b - a;
var d = a - b;

与数字一样，加一个向量的负值等于减去它的正值。

// These both give the same result.
var c = a - b;
var c = a + -b;

向量的负值具有与原始相同的模量，并且在同一直线上但方向正好相反。

从一个物体到另一个物体的方向和距离

如果从空间中的一个点减去另一个点，那么结果是“指向”一个物体的向量

// Gets a vector that points from the player's position to the target's.
var heading = target.position - player.position;

除了指向目标物外，这个向量的模量等于两个位置之间的距离。您可能需要一个“归一化”的向量来给定指向目标的方向，但有一个固定的距离（例如，用于指向一个投射物）。您可以通过除以向量的模量来归一化一个向量

var distance = heading.magnitude;
var direction = heading / distance; // This is now the normalized direction.

这种方法比分别使用模量和归一化属性更可取，因为它们都相当占用CPU资源（它们都涉及到计算平方根）。

如果您只需要使用距离进行比较（例如接近检查），那么您可以完全避免计算距离。sqrMagnitude属性提供了距离值的平方，其计算方法与距离相同，但省略了耗时的平方根运算。您不必将距离与已知距离进行比较，而是可以将距离的平方与距离的平方进行比较：

if (heading.sqrMagnitude < maxRange * maxRange) {
    // Target is within range.
}

这种方法比使用实际距离进行对比要高效得多。

有时，在3D工作中，您可能需要一个到目标的“地面航向”。例如，想象一个玩家站在地面上，需要接近空中漂泊的目标。如果从目标位置减去玩家位置，则得到的向量将指向目标上方。这对玩家移动的转向不适合，因为它们也将指向上方；真正需要的是从玩家位置到目标下方地面位置的向量。您可以通过将减法的结果的Y坐标设置为0来获得它：

var heading = target.position - player.position;
heading.y = 0;  // This is the overground heading.

标量乘法和除法

在讨论向量时，通常用一个普通数字（例如，一个浮点值）称为标量。标量的意思是它只有“刻度”或大小，而向量既有大小又有方向。

将向量乘以标量会导致一个向量，其方向与原始向量相同。然而，新向量的尺寸等于原始向量尺寸乘以标量值。

同样，标量除法将原始向量的尺寸除以标量。

这些运算对于向量表示移动偏移或力时很有用。它们允许您在不影响其方向的情况下改变向量的尺寸。

当任何向量除以其本身的大小，结果是一个具有尺寸1的向量，这称为规范化向量。如果将规范化向量乘以标量，则结果的大小将等于该标量值。这在力方向恒定但强度可控制时很有用（例如，车轮的推力始终向前推动，但力量是由驾驶员控制的）。

点积

点积是取两个向量的乘积，并返回一个标量。这个标量等于两个向量的尺寸相乘的结果乘以向量之间角度的余弦值。当两个向量都是归一化的时候，余弦值实际上指出第一个向量在第二个向量方向上的延伸程度（或相反 - 参数的顺序并不重要）。

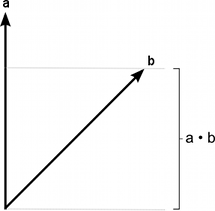
以下显示了不同角度的向量与参考向量比较返回的标量值在1和-1之间

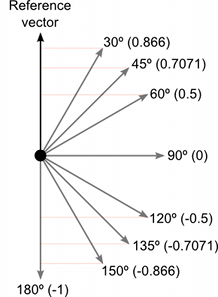
点积的计算比计算余弦值要简单，所以它可以在某些情况下取代Mathf.Cos功能或向量大小运算（它并不完全一样，但有时效果相当）。然而，计算点积函数所占用的CPU时间要少得多，因此它可以是一种有价值的优化。

当您想计算一个向量沿另一个向量方向的尺寸时，点积很有用。

例如，汽车的速度表通常通过测量车轮的转速工作。汽车可能并不是直接向前移动（例如可能是在侧滑）在这种情况下，部分运动不会在汽车面对的方向上——因此不会被速度表测量。物体刚体（rigidbody允许GameObject受到模拟的重力和其他力影响的组件。 更多信息
在词汇表中查看）的位移向量将给出其整体运动方向的速度，但要隔离正前方的速度，你应该使用点积。

var fwdSpeed = Vector3.Dot(rigidbody.velocity, transform.forward);

当然，方向可以是任何你喜欢的，但在此计算中，方向向量必须始终标准化。这不仅比速度的模长更准确，而且避免了寻找模长时涉及的慢速平方根运算。

叉积

叉积仅适用于三维向量。它接受两个三维向量为输入，并返回另一个三维向量为结果。

结果向量垂直于两个输入向量。你可以使用“右手螺旋规则”来记住输出向量的方向，该方向由输入向量的顺序确定。如果你可以按照输入向量的顺序弯曲手指，你的拇指指向输出向量的方向。如果参数的顺序被反转，则结果向量将指向完全相反的方向，但具有相同的模长。

结果向量的模长等于输入向量的模长相乘后乘以它们之间的正弦值。以下显示了正弦函数的一些有用值：

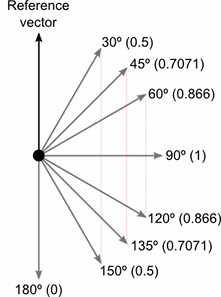
由于叉积在返回值中组合了几个有用的信息，因此它可能看起来很复杂。然而，就像点积一样，它在数学上非常有效，可以用来优化依赖于较慢的超越函数（如正弦和余弦）的代码。

计算法向量和垂直向量

在网格Unity的主要图形原语。网格构成了你的3D世界的大部分。Unity支持三角化或多边形网格。Nurbs、Nurms、子表面必须转换为多边形。 更多信息
在词汇表中查看生成过程中经常需要“法向量”（即垂直于平面的向量），它也在路径跟随和其他情况下很有用。给定平面上的三个点，例如网格三角形的角落点，你可以如下找到法向量：- 选择三个点中的一个 - 从剩下的两个点中分别减去它（得到两个新的向量，“Side 1”和“Side 2”） - 计算向量的叉积 - 叉积的结果是一个新向量，该向量垂直于这三个原始点所在的平面——这就是“法向量”。

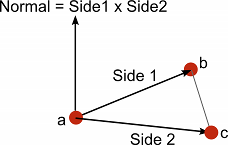
Vector3 a;
Vector3 b;
Vector3 c;

Vector3 side1 = b - a;
Vector3 side2 = c - a;

Vector3 normal = Vector3.Cross(side1, side2);

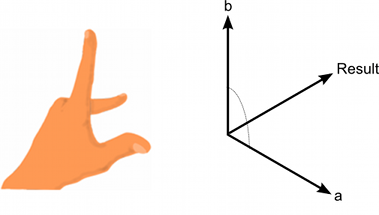
可以使用“左手规则”来确定将两个向量传递给叉积函数的顺序。当你从表面顶部向下看（从正常向量指向外部）时，第一个向量应该以顺时针方向环绕到第二个向量。

如果输入向量的顺序被颠倒，结果将指向完全相反的方向。

对于网格，法向量也必须被标准化。这可以通过使用归一化属性来完成，但也有另一种有时有用的技巧。你还可以通过除以它的模长来归一化垂直向量：

float perpLength = perp.magnitude;
perp /= perpLength;

另一个有用的提示是，三角形的面积等于perpLength / 2。这在你需要找到整个网格的表面积或想要基于它们的相对面积随机选择三角形时很有用。